Distanzvektor Routing-Protokolle

Beim Distanzvektoralgorithmus handelt es sich um einen dynamischen Routing-Algorithmus. Intern basiert der Distanzvektoralgorithmus auf den Bellman-Ford-Algorithmen. Dieser Algorithmus, benannt nach seinen Erfindern Richard Bellman und Lester Ford, dient zur Berechnung des kürzesten Weges ausgehend von einem Startknoten. Distanzvektor Routing-Protokolle geben in periodischen Abständen (etwa alle 30 Sekunden, bzw. bei einer Änderung der Topologie) die gesamte Kopie der eigenen Routing-Tabelle an ihren Nachbarn weiter. So werden Topologien Änderungen ausgetauscht.

Das Austauschen der Routing-Tabellen muss man sich folgendermaßen vorstellen: Router A gibt seine Informationen zu Router B weiter. Dieser Router B gleicht die neuen Informationen von Router A mit seinen vorhandenen Informationen ab und fügt schließlich seine Distanzvektornummer (z.B. Anzahl der Hops) hinzu. Nun gibt Router B die „aktualisierte“ Routing-Tabelle an Router C weiter. Dieser Vorgang wiederholt sich bei jedem benachbarten Router. Zu beachten ist dabei aber, das im Gegensatz zum Link-State-Algorithmus, nicht die gesamte bzw. genaue Topologie den Routern bekannt ist.

Bildlich lässt sich das Distanzvektor-Routing folgendermaßen beschreiben: Man stellt sich vor man möchte an einen Ort fahren. Nach den ersten Kilometer folgt das erste Schild, das einen Hinweis gibt in welche Richtung sich das Ziel befindet und vor allem wie viel Kilometer noch bis zum Ziel gefahren werden müssen. Etwas später folgt ein weiteres Schild, wieder mit dem gleichen Ziel, allerdings diesmal mit einer geringern Entfernung. Man bleibt dabei immer auf den besten Weg, während die Entfernung immer abnimmt, bis man schließlich das Ziel erreicht.

Zu Distanzvektorprotokollen gehören:

RIP (Routing Information Protocol)
IGRP (Interior Gateway Routing Protocol)

Neben dem Distanzvektoralgorithmus existiert noch der Link-State-Algorithmus, zu dem sich die zwei Link-State-Routing Protokolle IS-IS und OSPF zähen.

Nachfolgend ein gutes Beispiel eines Vorganges von de.wikipedia.org

Man geht von eine folgenden Konstellation aus:

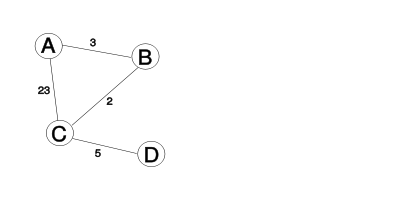
Distanz Vektor

Es existieren vier Router die wie in der obrigen Abbildung verbunden sind. In den nun folgenden Tabellen sind jeweils die Kosten abgebildet. Grün sind dabei die besten Pfade zu den jeweiligen Routern, während Gelb ein neuer bester Pfad - der im nächsten Schritt an die Nachbarn gesendet wird.

Nun folgen vier Schritte aus der Sicht des Router A. Im ersten Schritt, T=0, wird zu erst einmal eine Kostentabelle erzeugt und gleichzeitig werden die Informationen über die besten Pfade (B und C) weiter geschickt. Beim zweiten Schritt T=1 erhalten wir Datenpaktete von B und C und wissen nun wie wir D und C über B auch erreichen können. Im Fall der Zielrouter C und D ist das sogar ein neuer bester Pfad. Diese neuen Informationen werden dann wieder an die Nachbar-Router übertagen. Im dritten Schritt T=2 erreicht uns ein Paket von Router B, das uns mitteilt dass B den Router D günstiger erreichen kann. Auch diese Informationen werden weiter verschickt, nachdem wir sie in unsere Routing-Tabelle aufgenommen haben. Im letzten Schritt T=3 bleibt alles so wie es war, da keine neue Routing Informationen verschickt wurden. D.H. es wird nichts in der Routing Tabelle geändert und es wird nichts weiter geschickt.

T=0

von A	via B	via C
zu A
zu B	3
zu C		23
zu D

von B	via A	via C
zu A	3
zu B
zu C		2
zu D

von C	via A	via B	via D
zu A	23
zu B		2
zu C
zu D			5

von D	via A	via B	via C	via D
zu A
zu B
zu C			5
zu D

T=1

von A	via B	via C
zu A
zu B	3	25
zu C	5	23
zu D		28

von B	via A	via C
zu A	3	25
zu B
zu C	26	2
zu D		7

von C	via A	via B	via D
zu A	23	5
zu B	26	2
zu C
zu D			5

von D	via A	via B	via C	via D
zu A			28
zu B			7
zu C			5
zu D

T=2

von A	via B	via C
zu A
zu B	3	25
zu C	5	23
zu D	10	28

von B	via A	via C
zu A	3	7
zu B
zu C	8	2
zu D	31	7

von C	via A	via B	via D
zu A	23	5	33
zu B	26	2	12
zu C
zu D	51	9	5

von D	via A	via B	via C	via D
zu A			10
zu B			7
zu C			5
zu D

T=3

von A	via B	via C
zu A
zu B	3	25
zu C	5	23
zu D	10	28

von B	via A	via C
zu A	3	7
zu B
zu C	8	2
zu D	13	7

von C	via A	via B	via D
zu A	23	5	15
zu B	26	2	12
zu C
zu D	33	9	5

von D	via A	via B	via C	via D
zu A			10
zu B			7
zu C			5
zu D